哈尔滨工业大学数学系2015博士招生复试大纲
理学院数学系博士入学考试
——导师考核及专家小组考核大纲
一、导师考核部分
导师考核内容自定，可以采用笔试或面试方式，满分100分。
二、专家小组考核部分
数学系专家小组考核采用笔试、面试相结合的考核方式，全面考评考生的基本专业知识掌握、基本原理掌握及分析问题和解决问题的能力。满分共100分。
其中，面试考核满分为50分，主要考评考生的表达能力、逻辑思维能力、外语能力，以及所从事的工作或研究经历等内容。
笔试考核满分为50分，考试大纲如下：
(一)考试要求
1.报考“数学”专业考生，在以下4个科目
“泛函分析”、“抽象代数”、“现代数值分析”、“概率论”
中选择二个科目(专业基础与专业综合不能选同名的科目)，每科25分，共50分。
2.报考“统计学”专业考生，在以下3个科目
“数理统计”、“概率论”、“现代数值分析”
中选择二个科目(专业基础与专业综合不能选同名的科目)，每科25分，共50分。
3.各科目要求：要求考生全面系统地掌握所选科目的基本知识，具备较强的分析问题与解决问题的能力。
(二)考试内容
1.泛函分析：
1) 度量空间、赋(准)范线性空间、内积空间的基本定义，基本定理，基本性质及这些空间的具体例子;凸集与Minkowski泛函的定义及基本性质。
2) 算子和泛函的线性性、有界性、连续性的定义、关系、基本性质;Riesz定理及应用。
3) 纲，开映像定理与闭图像定理及推论(含Banach逆算子定理等)，共鸣定理及应用。
4) 线性泛函的延拓定理及其几何形式。
5) 共轭空间(含例子)与共轭算子，以及二次共轭空间与空间的自反性，弱收敛及弱* 收敛，弱列紧性及弱*列紧性。
6) 线性算子的譜的定义和例;紧算子的定义和基本性质。
2.抽象代数：
1) 群论：在掌握群、子群、正规子群、商群等概念和有关性质及群同态基本定理的基础上，要求应试者进一步了解与掌握：作用在集上的群;p群•Sylow子群;可解群与Jordan-Holder定理;有限生成Abel群的结构。
2) 环论：在掌握环、子环、理想、商环等概念和有关性质及环同态基本定理的基础上，要求应试者进一步了解与掌握：交换环中的素理想、极大理想的基本性质，交换环中的可逆元，幂等元，零因子等的基本性质;交换环的大根与小根;有关交换环的局部化理论;链条件;分式理想与类群。
3) 模论：模与模同态;Hom与
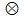;直积与直和;自由模、投射模、入射模;正合列与交换图;一些特殊环上的模。
4) 域论：单纯扩张与有限扩张;分裂域，正规扩张;可离扩张;有限域;有限扩张的单纯性。
5) Galois 理论：Galois群;域与群的结对关系;多项式的Galois群。
3.现代数值分析：
1) 数值逼近：多项式插值、样条插值、有理插值;正交多项式的性质及构造方法;最佳一致逼近、最佳平方逼近、曲线拟合的最小二乘法。
2) 数值积分与微分：高斯型求积公式的一般理论;奇异积分与振荡函数积分数值计算;数值微分公式的构造方法。
3) 线性代数方程组数值解法：直接解法;矩阵的条件数与扰动方程组的误差界估计;迭代解法的方法构造及收敛性判定;共轭梯度法。
4) 非线性方程组数值解法：牛顿法及其变形方法、拟牛顿法。
5) 常微分方程数值解法：初值问题数值解法(单步法的收敛性与稳定性、线性多步法);边值问题数值解法(打靶法、差分法)。
4.概率论：
1) 集类与单调类定理，测度与概率，测度的扩张定理及测度的完备化，独立事件类。
2) 随机变量与可测函数，分布函数，独立随机变量，随机变量序列的收敛性。
3) 积分的定义和性质，收敛定理，数学期望，不定积分与
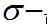可加集函数的分解。
4) 有限维乘积测度，Fubini定理。
5) 条件概率与条件数学期望，正则条件概率。
5. 数理统计：
1)预备知识：
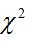分布、t 分布和F 分布，指数分布族，条件期望和条件概率，统计判决的基本概念，充分统计量和完备统计量;
2)点估计: 无偏估计，Cramer-Rao型不等式，Bayes估计和Minimax估计，不变估计与可容许估计，大样本理论的基本概念， 矩估计和极大似然估计，序贯点估计;
3)假设检验: 基本概念，一致最优检验, 一致最优的无偏检验，不变检验，拟合优度检验，似然比检验，序贯检验;
4)区间估计：置信区间，Bayes方法和信仰推断法，序贯区间估计;
5)线性模型: 最小二乘估计,线性假设检验与可估函数的区间估计，回归分析, 方差分析，协方差分析.线性估计类，大样本理论，矩阵的广义逆;
6)非参数统计: 次序统计量与极值分布，U-顺序统计量, 秩次统计量，置换检验，非参数检验的功效。
(三)试卷结构
1.考试时间120分钟，满分50分。
2.各科目试题结构：每个科目出5个题目，每个题目5分，其中有些考查基本概念、基本理论的掌握情况，有些考查基本理论的应用和理论推导的能力。
(四)参考书目
1.“泛函分析”科目：
张恭庆等，《泛函分析》上册， 北京大学出版社
2.“抽象代数”科目：
1)T. W. Hungerford，《Algebra》，Springer-Verbag
2)张海权、游宏，《抽象代数》，东北师大出版社
3.“现代数值分析”科目：
李庆扬、关治、白峰杉，《数值计算原理》，清华大学出版社，2000
4.“概率论”科目：
严士健等，《概率论基础》，科学出版社
5. “数理统计”科目：
1)陈希孺著，《数理统计引论》，科学出版社,1997年8月
2)陈希孺著，《高等数理统计学》，中国科学技术大学出版社，1999年2月
注意：本文归作者所有，未经作者允许，不得转载
